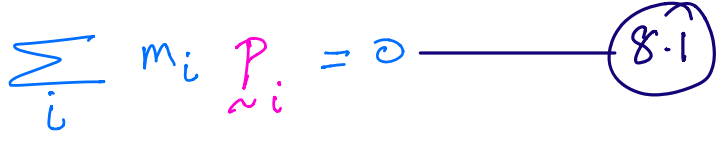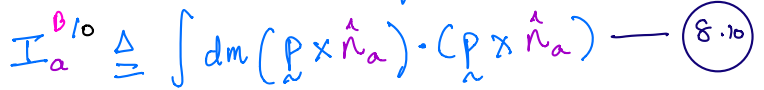Mass/Inertia Scalars¶
Mass: measure of amount of materia in a body. Units of measurement: \(kg\), \(lb\).
Mass center: consider a set of particles as shown below which together make up the system of particles \(S\):
The \(i^{\text{th}}\) particle has a mass \(m_i\)
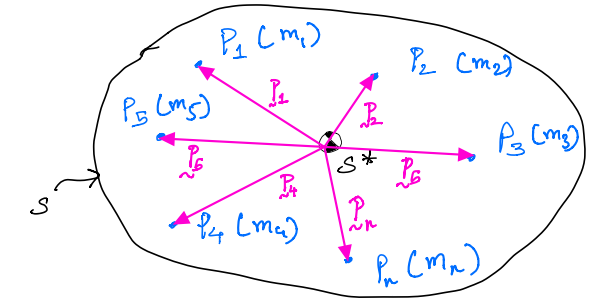
\(S^*\) is a fictitious particle such that:
This fictitious particle is called mass center.
How does one locate the mass centre from a point \(O\)?
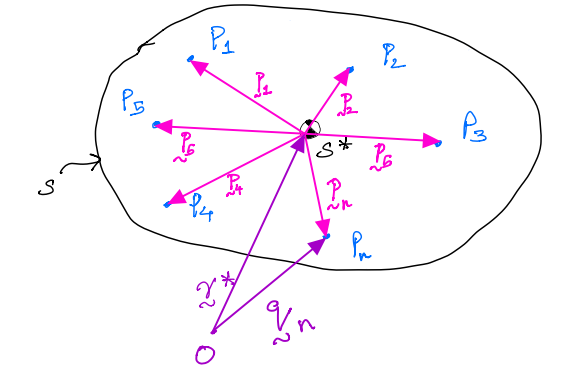
\(r^*\); position vector from \(O\) to \(S^*\)
\(q_n\); position vector from \(O\) to \(P_n\)
So, we have,
So, expanding 8.1

For a continuum:
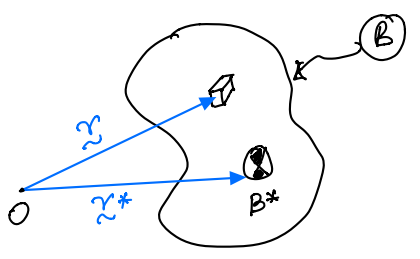
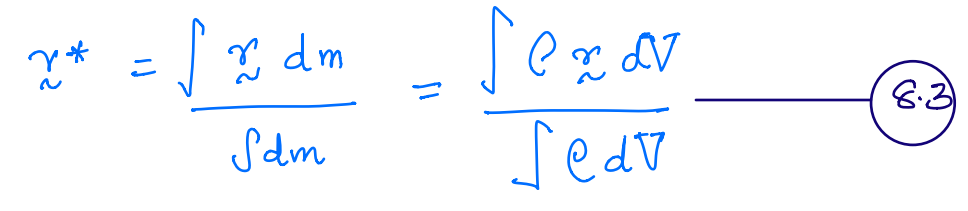
where, \(dm\) is elemental mass that can be obtained from density \(\rho\) and elementar volume \(dV\).
Composite theorem for mass centre¶
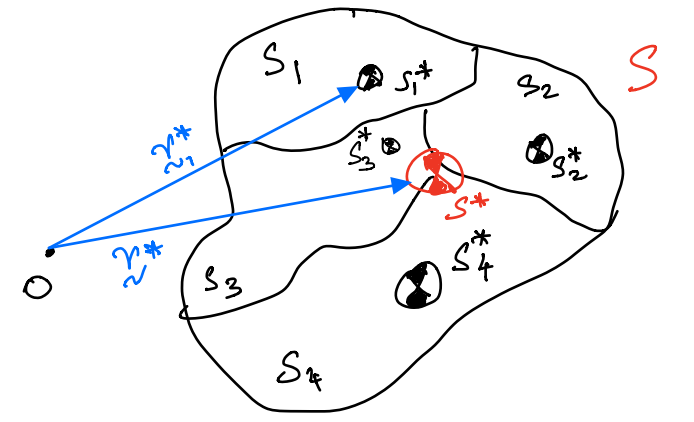
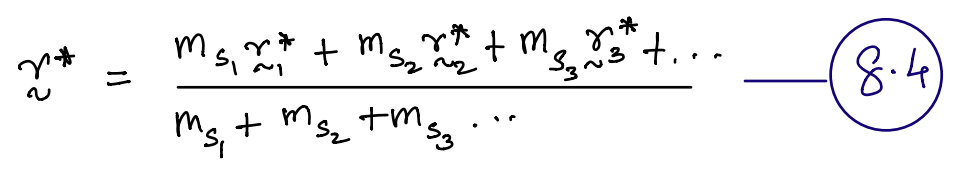
where,
\(r^*_i\) is the position vector locating the mass centre of \(S_i\), the \(i^{\text{th}}\) system of particles.
\(m_{s_{i}}\) is the mass of \(i^{\text{th}}\) system.
\(r^*\) is the mass centre of the composite system \(S\).
Example #1¶
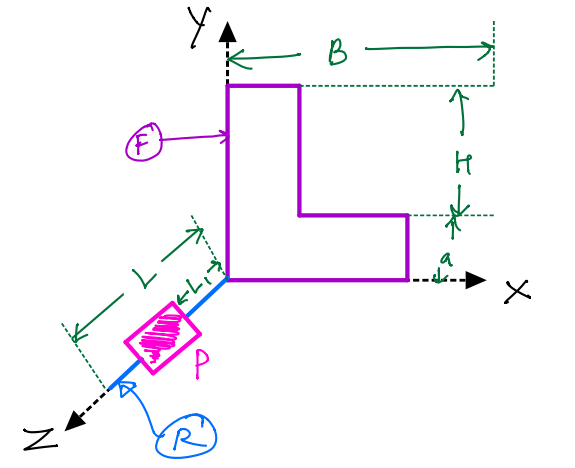
Given:
\(F\) and \(R\) are the bodies of mass density \(\rho\; kgm^{-2}\) and \(\sigma\;kgm^{-1}\) respectively.
\(P\) is a particle of mass \(m\).
Find:
Mass centre of the combined system.
Example #2¶
\(F\) is split into two: \(F_1\) and \(F_2\).
\(m_{F_{1}}\) = \(\rho H_a\), is mass of \(F_1\).
\(m_{F_{2}}\) = \(\rho B_a\), is mass of \(F_2\).
Also,
\(m_{R}\) = \(\sigma L\), is mass of \(R\).
Then,
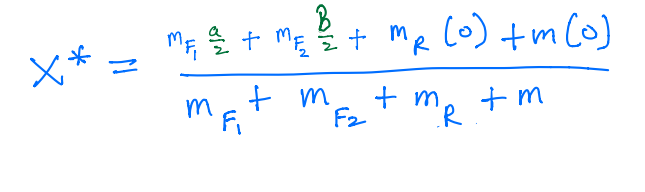
Similarly,
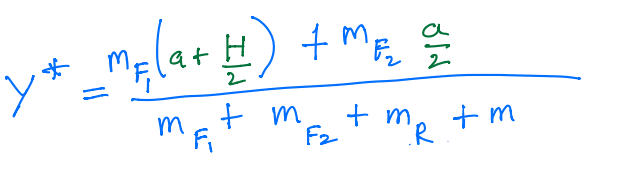
and
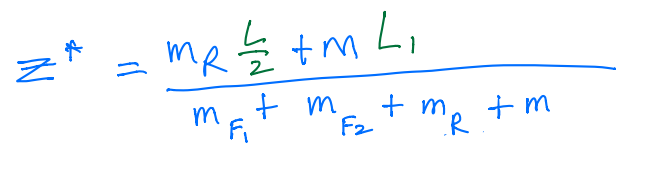
Inertia scalar¶
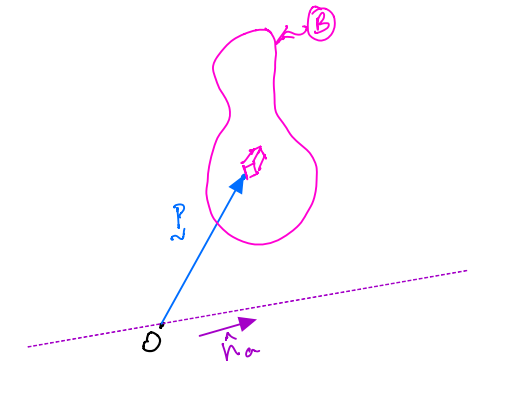
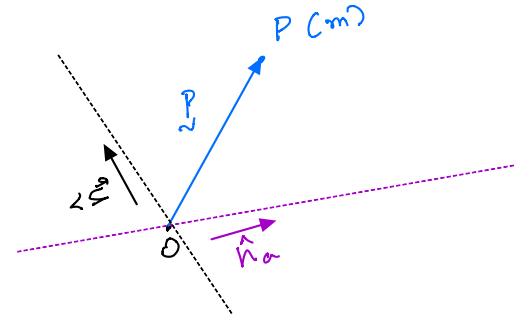
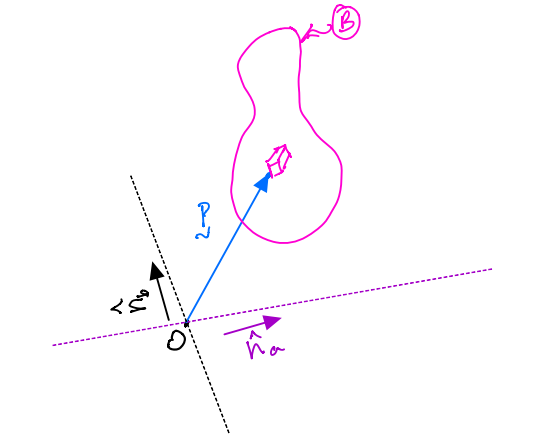
For a particle \(P\) of mass \(m\), we can define a parameter called the inertia scalar. This is defined relative to an arbitrary point \(O\). There are two such inertia scalars:
Product of inertia¶
Notation¶
\(I^{P/O}_{ab}\) is the product of inertia of \(P\) along two lines through point \(O\) that are parallel to unit vectors \(\hat{n}_a\) and \(\hat{n}_b\).
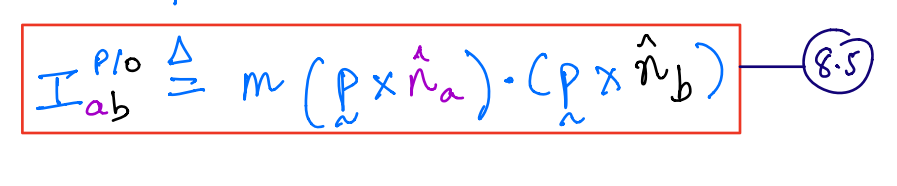
8.5 can be extended for both systems of particles and continua.
Product of inertia of system particles¶
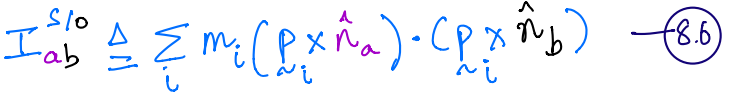
Product of inertia of continua¶
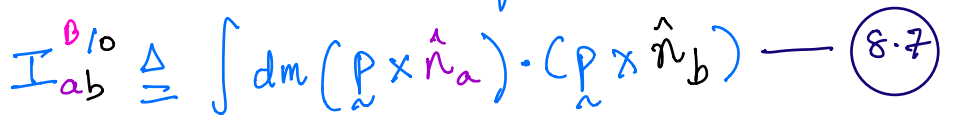
Warning
In all cases, \(I_{ab} = I_{ba}\) because the formula relies on the dot product of vectors.
2. Moment of inertia¶
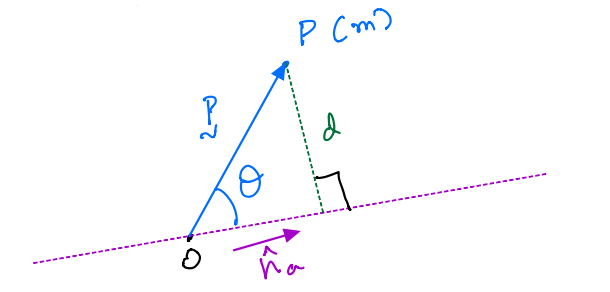
Notation¶
\(I^{P/O}_{aa}\) is the moment of inertia of P about a line through point \(O\) which is parallel to the unit vector \(\hat{n}_a\).
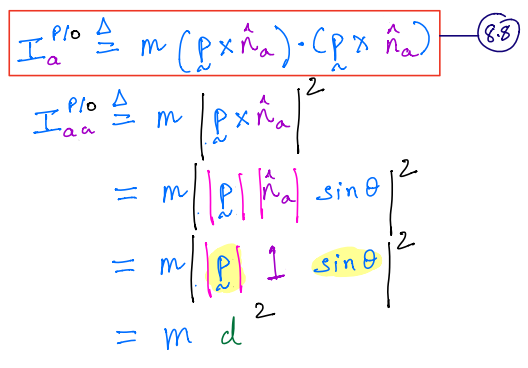
8.8 can be extended to both systems of particles and continua.
Product of inertia of system of particles¶
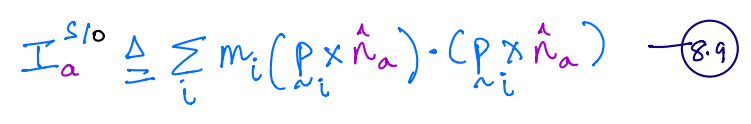
Example¶
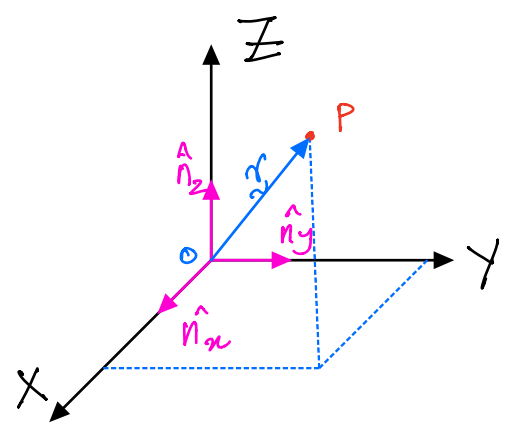
\(P\) is a particle of mass \(m\).
\(\hat{n}_x,\;\hat{n}_y,\;\hat{n}_z\) are unit vecotrs that are mutually orthogonal.
\(\vec{r} = x\hat{n}_x + y\hat{n}_y + z\hat{n}_z\)
Find:
Solution
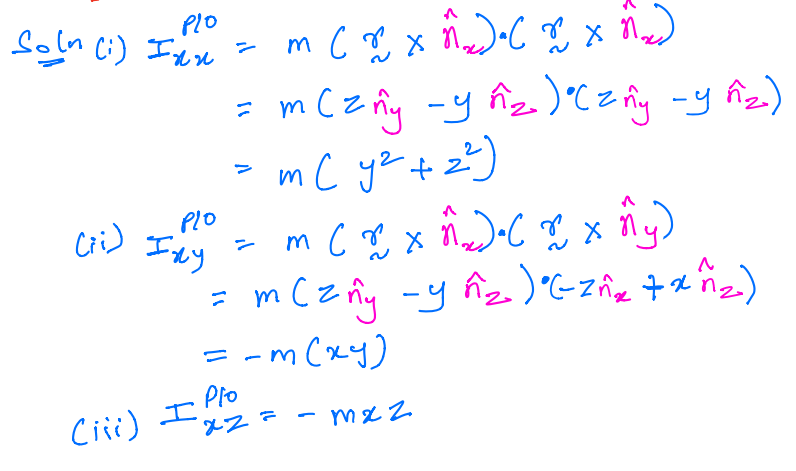
From inertia scalars to inertia matrix¶
From the previous example, we now have some insight that we will be interested in computing the moments of inertia and products of inertia about a set of unit vectors that make up a reference frame.
For this discussion, we assume that the unit vectors are: \(\hat{n}_x,\;\hat{n}_y,\;\hat{n}_z\).
The inertia scalars can be used to define a square matrix called the inertia matrix.
Notation:
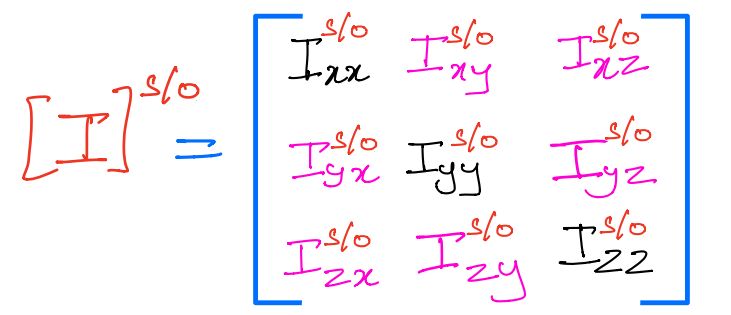
\(\left[I\right]^{S/O}\) is the inertia matrix of \(S\), a system of particles about the point \(O\).
The diagonal elements of this matrix are the moments of inertia.
The off-diagonal elements are the products of inertia.
So, the inertia matrix is represented as:
Warning
In all cases, \(I_{ab} = I_{ba}\) because the formula relies on the dot product of vectors.
Rigid body/ continua: The inertia scalars of a rigid body can also be arranged into an inertia matrix.