Contents

Key Theorems for computing \(\left[I\right]^{S/O}\)

There are three useful theorems to compute moments of inertia. They are:

  1. Rotation theorem

  2. Parallel axis theorem (or translation theorem)

  3. Composite theorem

Let us examine them in further detail.

Rotation theorem

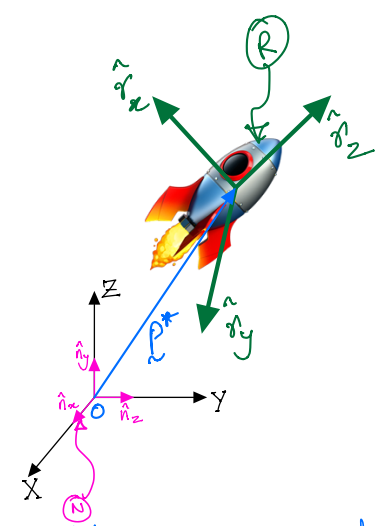
../_images/261.png

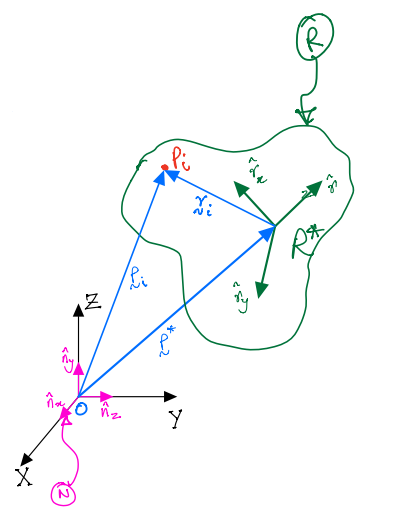
  • \(X-Y-Z\) make up a cartesian coordinate system.

  • \(O\) is the origin.

  • \(\hat{n}_x,\;\hat{n}_y,\;\hat{n}_z\) are unit vectors directed along \(X-Y-Z\) respectively. The unit vectos represent a reference frame \(N\).

Also, the figure shows a rocket which has a reference frame \(R\) attached to it. You are given the inertia matrix of the rocket \(R\) about \(O\) along the unit vectors of frame \(N\). Naturally, this reference frame also has \(3\) mutually orthogonal unit vectors:

\[ \hat{r}_x \qquad \hat{r}_y \qquad \hat{r}_z \]
../_images/271.png

Now, we can define another inertia matrix for \(R\) about \(O\) along the newly introduced rotating reference frame’s unit vectors \(\hat{r}_x, \; \hat{r}_y, \; \hat{r}_z\). This matrix and its elements are:

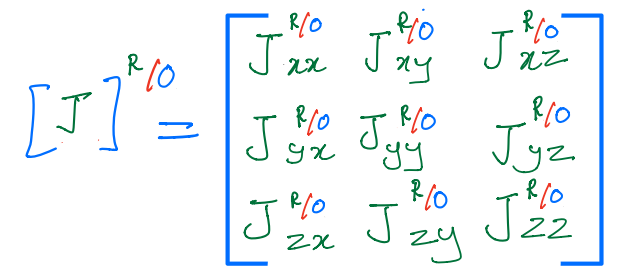
../_images/281.png

Question: How are the two matrices related?

We begin by assuming that \(R\) is a particle of mass, \(m_R\).

Let us consider a product of inertia from each matrix.

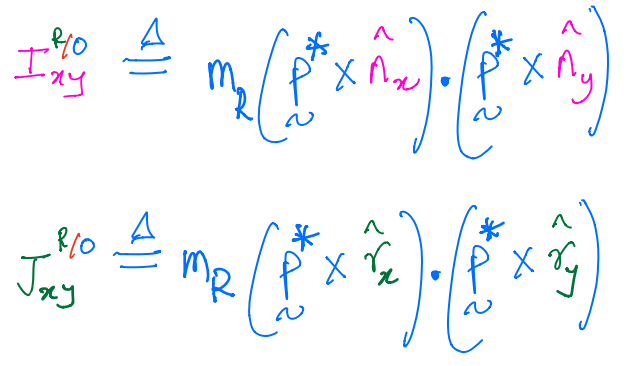
../_images/291.png

\(P^*\) is a position vector from \(O\) to the origin of the frame \(R\).

We know from our discussion on direction \(\text{cosine}\) matrices that the unit vectors of \(R\) can be related to the unit vectors of \(N\) as:

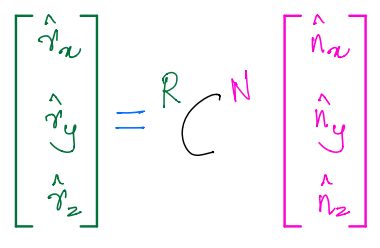
../_images/301.png

\({}^{R}C^{N}\) is the direction \(\text{cosine}\) matrix of \(R\) in \(N\). It is a \(3\times3\) matrix, which we shall assume has the following elements:

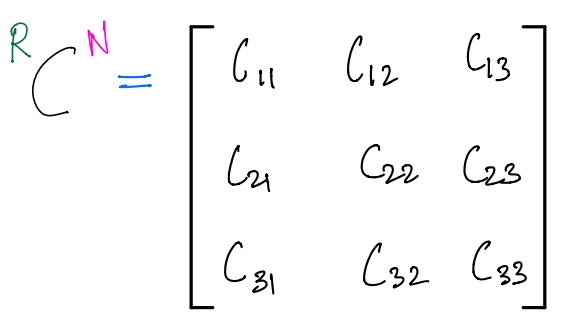
../_images/311.png

So, we can now easily derive:

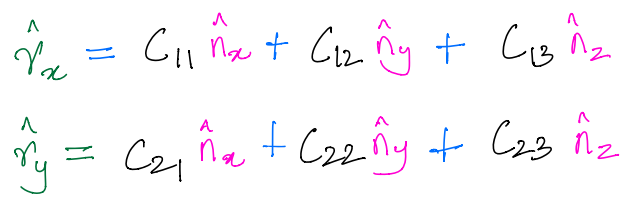
../_images/321.png

And then, we can rewrite the product of inertia \(J^{R/O}_{xy}\) as:

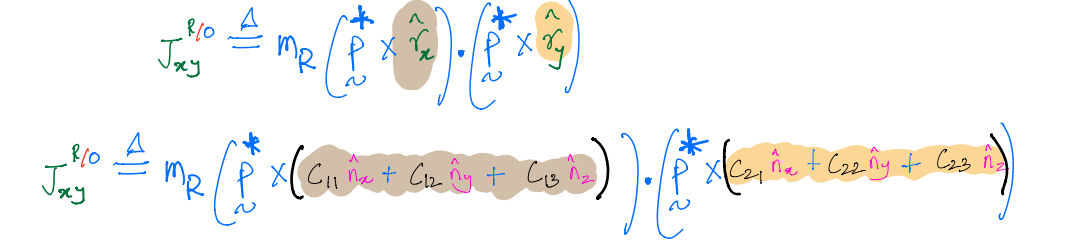
../_images/331.png

This leads to

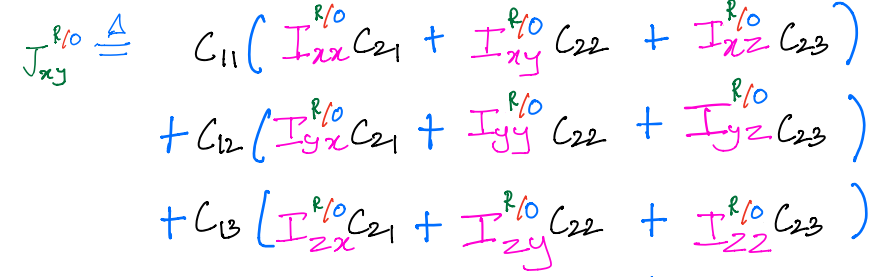
../_images/341.png

or in terms of matrix multiplication.

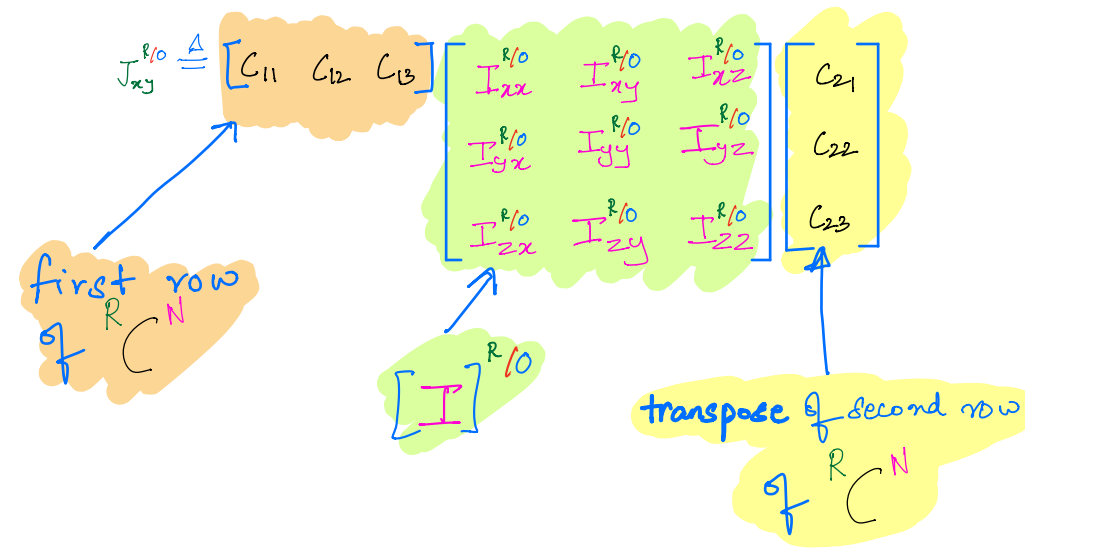
../_images/351.png

More generally, it can be shown that

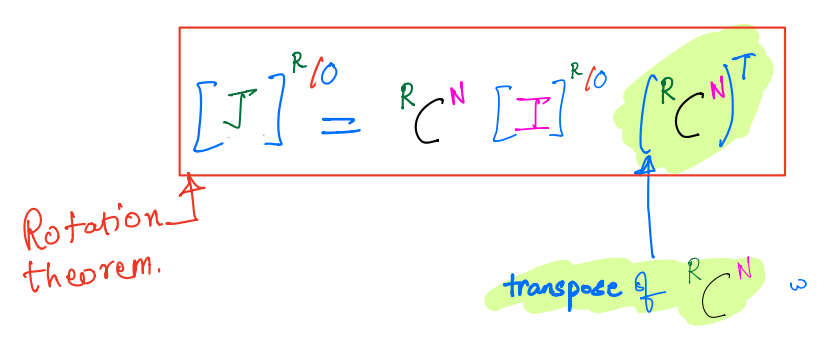
../_images/361.png

Parallel axes theorem

In the previoussection we presumed that the rocket was a point mass. What happens if this assumption is relaxed and rockets are better approximated as a system of particles?

  • \(P^*\) is a position vector from \(O\) to \(R^*\), the origin of the frame \(R\).

  • \(R^*\) is he mass center of the rocket.

  • \(\vec{P}_i\) is a position vector from \(O\) to \(\vec{P}_i\), the \(i^{\text{th}}\) particle on the rocket body.

  • \(r_i\) is a position vector from \(R^*\) to \(\vec{P}_i\). So,

\[ \vec{P}_i = P^* + r_i \]
../_images/371.png

Now, we know that the product of inertia for this system of particles along the \(\hat{n}_x,\;\hat{n}_y,\;\hat{n}_z\) directions given by:

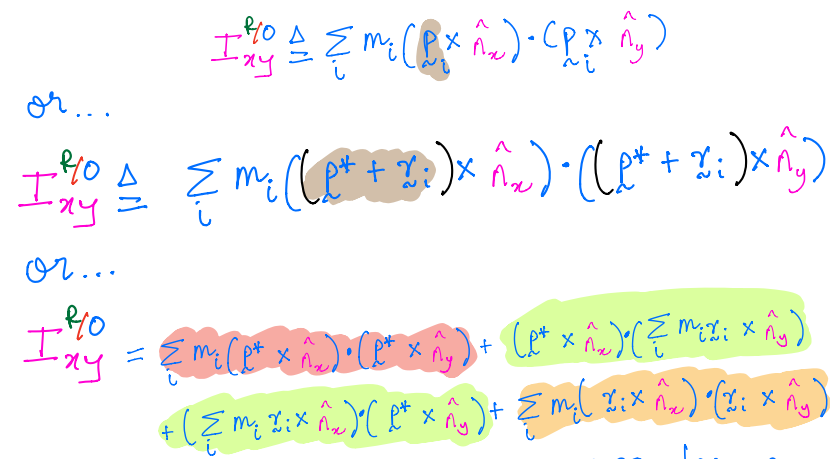
../_images/381.png

The terms highlighted in green go to zero because \(\sum_im_ir_i = 0\) by the definition of mass centers.

../_images/391.png

\(I^{R/R^*}_{xy}\) is the product of inertia of \(R\) about the mass center \(R^*\).

\(I^{R^*/O}_{xy}\)is the product of inertia of \(R^*\) about \(O\).

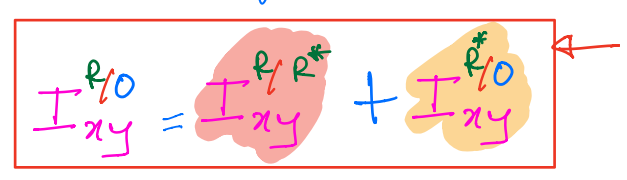
This result extrapolates to the moment of inertia scalars. For example,

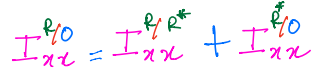
../_images/401.png

This result extrapolates to the inertia matrix,

../_images/411.png

This rule is only valid when going through the mass center.

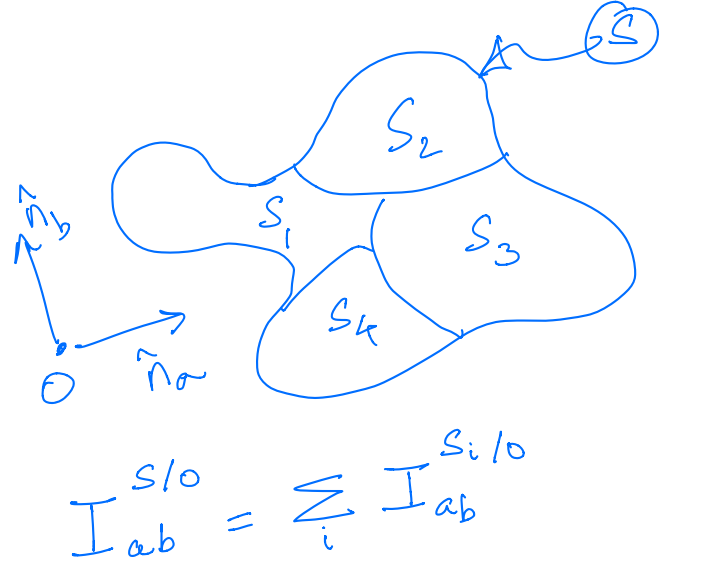
Composite theorem

../_images/421.png